Тема дробей — одна из самых непростых для школьников. Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.

Как объяснить суть дробей ребенку?

Слово «дробь» будто говорит само за себя — оно означает дробление, деление. В школьной программе к изучению дробей приступают только в 5 классе, освоив все действия с целыми числами. Но знакомство с ними целесообразно начинать заранее, еще в старшем дошкольном возрасте. Это формирует пространственные представления у детей и тренирует логическое мышление.

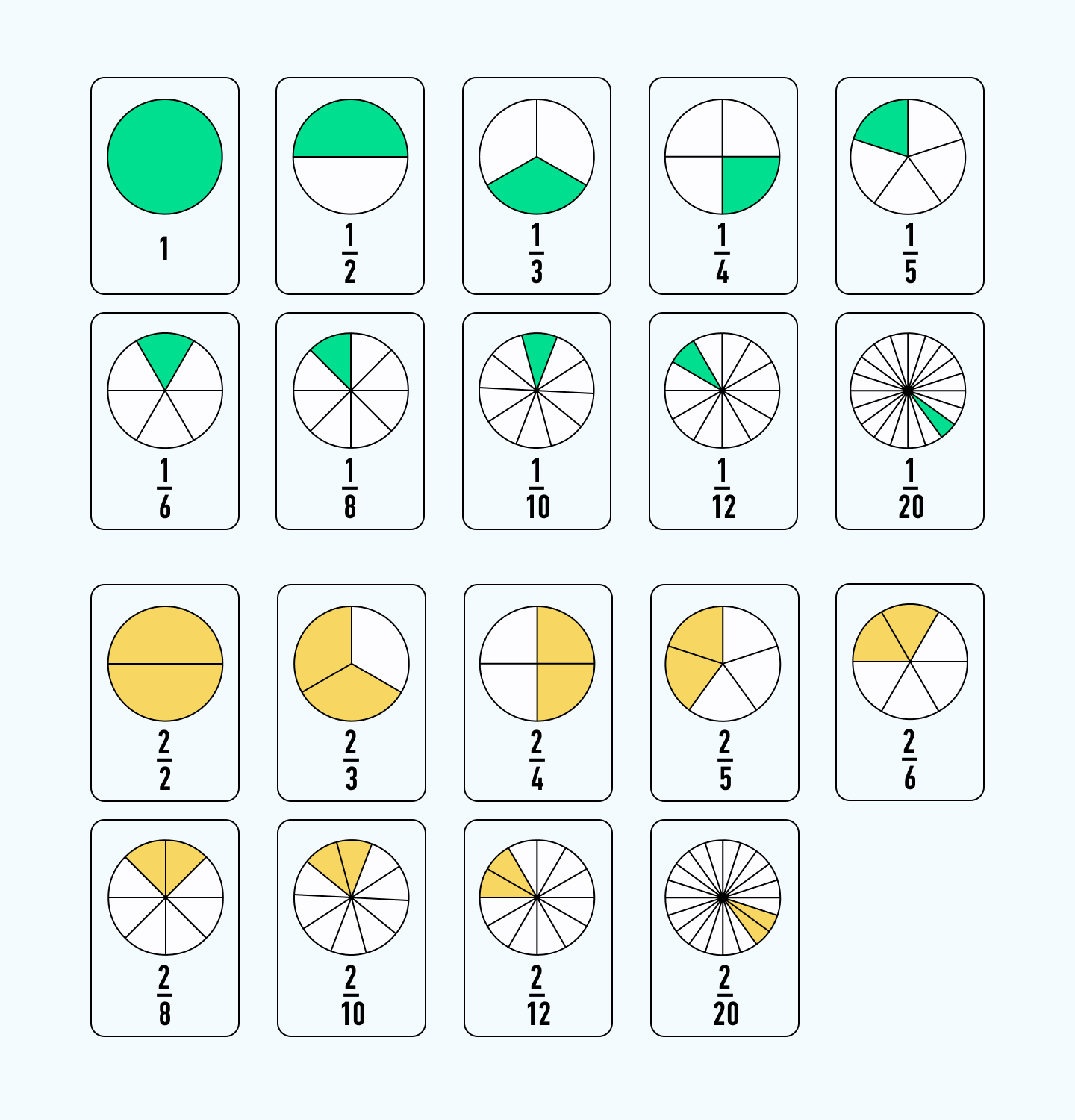
Для начала нужно объяснить ребенку понятие долей. Это очень легко сделать на наглядных повседневных примерах. Самый простой и доступный — еда. Например, пирог — целый. Разделить его можно на несколько одинаковых частей. Один кусочек такого пирога и будет называться одной долей из всех возможных. Поделив пирог на четыре части, один кусочек называют одной четвертой частью.

Таким образом делить можно все, что угодно: яблоки, апельсины, плитки шоколада, конфеты в коробке и т. д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.

Если ребенок увидит практическое применение дробей и востребованность их в реальной жизни, ему будет проще понять их и осознать важность получения математических знаний и навыков.

Что нужно знать о дробях?

1. Дробь — число нецелое, оно обозначает количество долей целого.

2. Дробь меньше целого.

3. Чем на большее число долей поделено целое, тем эти доли меньше и наоборот — чем долей меньше, тем они, соответственно, больше.

Для обозначения долей в математике используют понятие обыкновенная дробь. С ее помощью можно записать абсолютно любое необходимое количество долей.

Обыкновенная дробь представляет собой две части, именуемые числителем и знаменателем. Записываются они разделенными горизонтальной чертой либо наклонной вправо линией. Знаменатель пишется внизу либо справа от дробной черты, он показывает общее количество частей от целого, на которое оно было поделено. А числитель пишется вверху или слева от дробной черты и показывает, сколько долей целого сейчас взяли.

Вернемся к нашему пирогу. Очевидно, что разделить его реально на сколько угодно равных частей. В зависимости от того, на сколько частей его разделили, меняется и знаменатель дроби. У пирога, разделенного одной прямой линией на две части, знаменатель будет равен 2, у разделенного на три части — 3 и т. д. Числитель же, в свою очередь, показывает, сколько частей сейчас взято. Если взяли только одну часть из двух, то получится дробь 1/2, только две из трех — 2/3 и т. д.

Что такое смешанные дроби?

В математике выделяют дроби правильные и неправильные. Правильные — те, у которых числитель меньше знаменателя. Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.

У таких дробей можно отделить целую часть и оставшуюся после этого дробную. То есть будет видно, сколько взято целых пирогов и плюс определенное количество его частей. Нужно хорошо представить себе описанное, или даже проверить на практике, а не просто заучивать формулы. Тогда сокращение дробей будет выполняться ребенком осмысленно и безошибочно.

Для того чтобы трансформировать неправильную дробь в смешанное число, следует сперва числитель поделить на знаменатель. В результате почти всегда получим целое число и какой-то остаток. Целое число и нужно записать, как целую часть. А остаток — отправить в числитель дробной части. Неизменным остается только знаменатель.

Неправильными называют и дроби с одинаковым числом над и под дробной чертой: 6/6, 12/12 и т. д. Очевидно, что превратить их можно в 1. Наглядно это взято столько кусочков пирога, на сколько он и был поделен, т. е. целый пирог.

Примеры:

• 14/5 = (5*2+4) / 5 = 2 4/5
• 21/6 = (6*3+ 3) / 6 = 3 3/6

Задание:

Выделите целую часть из неправильных дробей:

• 15/4,
• 22/12,
• 30/7.

Можно провести противоположную процедуру — превратить смешанное число в неправильную дробь. Эта операция часто применяется в математических вычислениях, поэтому будет полезным узнать о ней. Для этого нужно сперва умножить целую часть и знаменатель. Затем получившееся число прибавить к числителю, а знаменатель оставить прежним.

Примеры:

• 3 1/8 = (3*8+1) / 8 = 25/8
• 7 4/9 = (7*9+4) / 9 = 67/9

Задание:

1. Преобразовать в смешанное число неправильную дробь:

• 27/4,
• 18/5,
• 45/7.

2. Выполнить обратную первой задачу — смешанное число превратить в неправильную дробь:

• 3 4/5;
• 12 7/11.

Десятичные дроби

Дроби, в знаменателях которых есть числа, кратные десяти — 10, 100, 1000 и т. д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.

Например, 5 4/10 попробуем записать в виде десятичной дроби. Пишем целую часть (5), ставим запятую и далее пишем числитель дробной части (4). Получаем: 5,4. Читается эта дробь так: «пять целых и четыре десятых». Число, представленное в таком виде, именуется десятичной дробью.

Существуют также десятичные дроби без целой части. Например: 7/100. Как быть в таком случае? Чтобы записать подобную дробь, пишут ноль, ставят запятую и далее записывают числитель дроби — 0,07. Такая дробь читается как «ноль целых, семь сотых».

Десятичные дроби очень удобны, они используются в точных вычислениях. Десятичная система исчисления  применяется человечеством с самых древних времен. Она интуитивна понятна и проста.

Задание:

Преобразовать следующие дроби в десятичные:

• 8/10,
• 4/100,
• 7/1000.

Сокращение дробей

Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.

Пример 1. Сократить дробь 8/12

Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:

8/12 = 8:4 / 12:4 = 2/3

Пример 2. Сократить дробь 10/25

Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:

10/25 = 10:5 / 25:5 = 2/5

Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.

Задание:

Сократите следующие дроби:

• 6/18,
• 20/40;
• 7/21.

Сложение дробей

Сначала разберем сложение дробей с одинаковыми знаменателями. В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.

Примеры:

• 1/7 + 2/7 = 3/7
• 3/8 + 5/8 = 8/8 = 1

Задание:

Выполни сложение дробей с одинаковыми знаменателями:

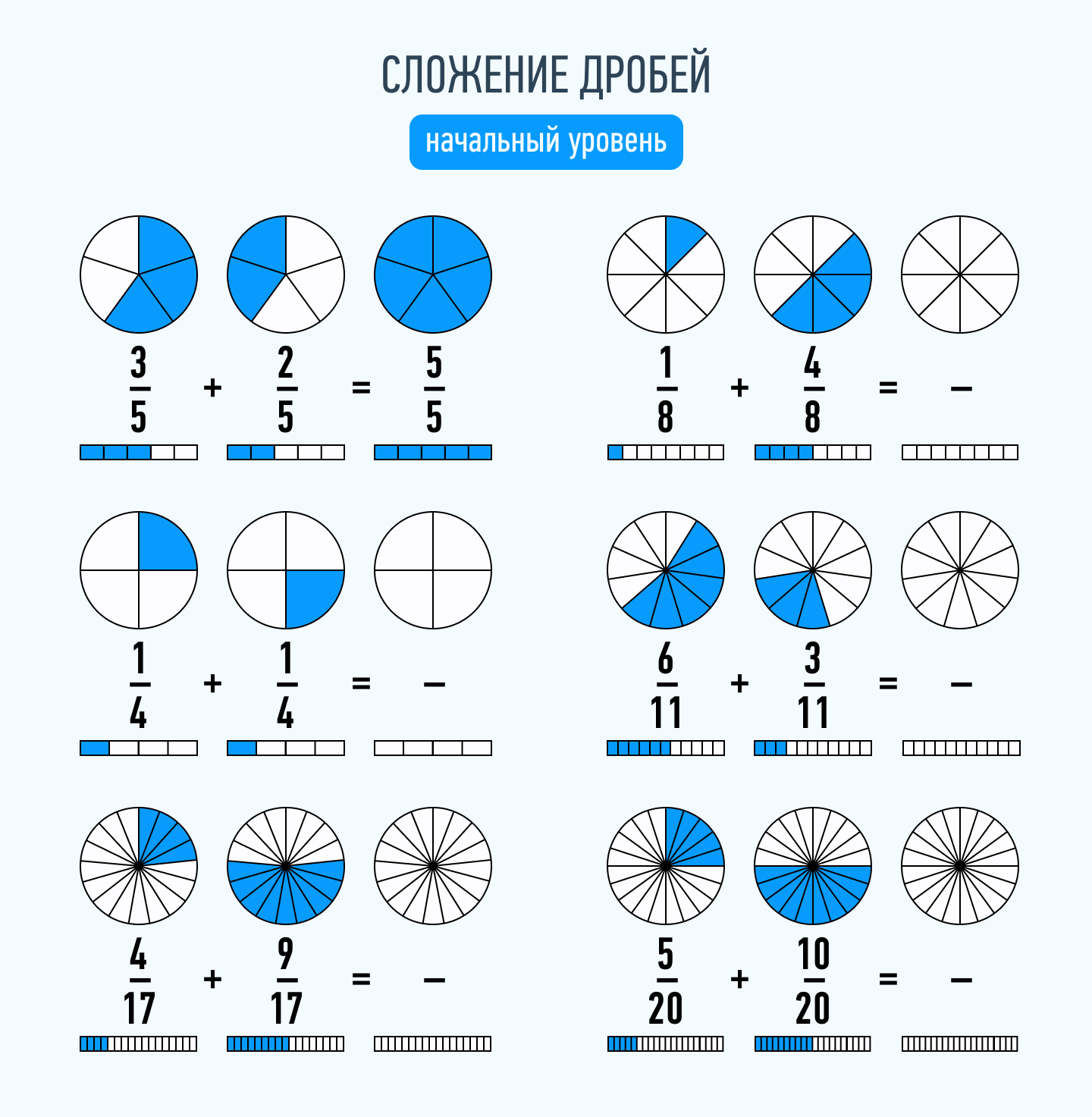
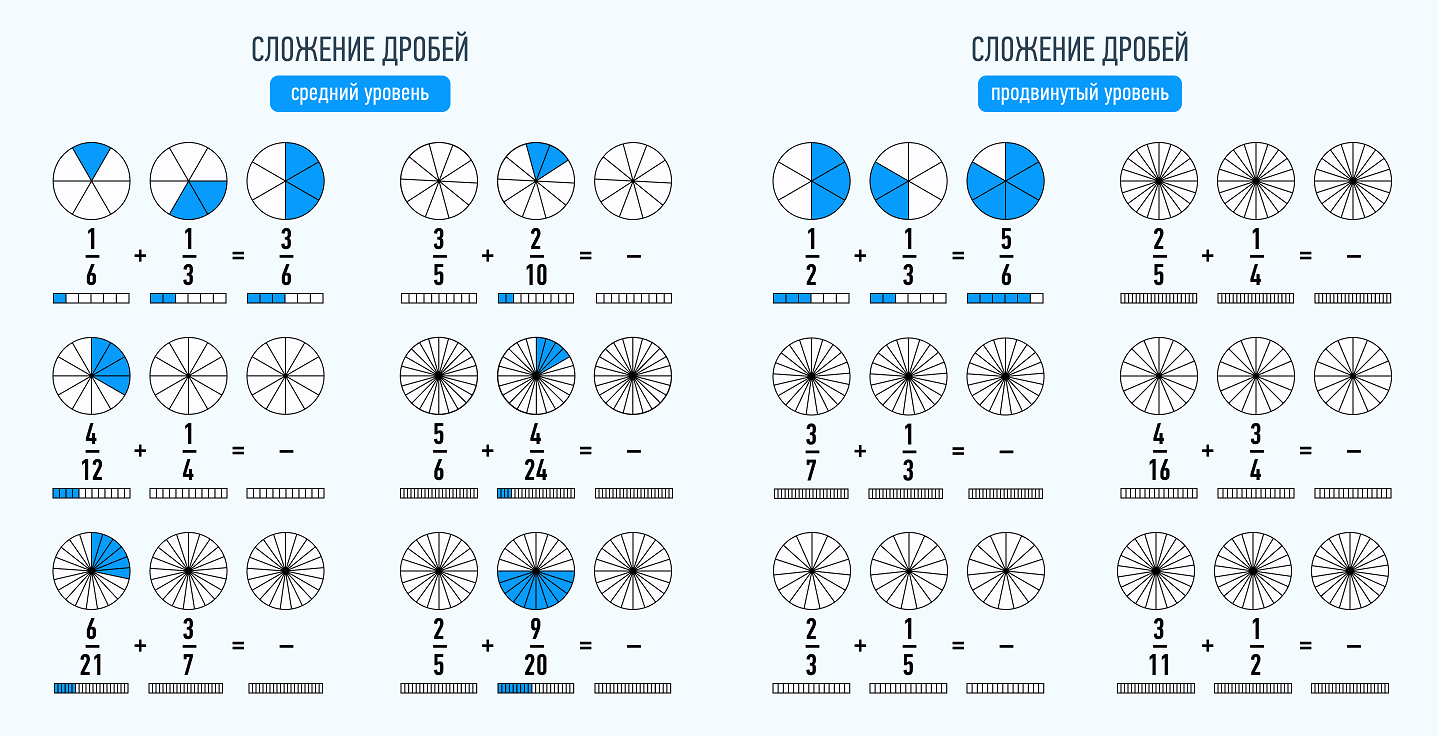
Но все усложняется, если нужно сложить дроби с разными знаменателями. В этом случае необходимо привести дроби к наименьшему общему знаменателю. Чтобы это сделать, необходимо найти наименьшее общее кратное. Это такое число, которое делится на оба эти числа без остатка. Например: 3/7 + 2/6. Наименьшее общее кратное для чисел 7 и 6 будет 42.

Далее ищем дополнительные множители для каждой из дробей. Для этого найденное на предыдущем этапе наименьшее общее кратное делим по очереди на знаменатель каждой из дробей:

• 42 / 7 = 6 — это будет дополнительный множитель для 3/7;
• 42 / 6 = 7 — это, соответственно, дополнительный множитель для 2/6.

Обе части каждой из наших дробей, и числитель и знаменатель, умножаем на свой, определенный выше, множитель:

• 3*6 / 7*6 = 18/42;
• 2*7 / 6*7 = 14/42.

Складываем полученные дроби аналогичным образом, как уже разобранные выше дроби с одинаковыми знаменателями:

• 18/42 + 14/42 = 32/42

Если это возможно, то дробь сокращают. Если дробь получилась неправильная, то следует целую часть из нее выделить.

Задание:

Выполни сложение дробей с разными знаменателями:

Вычитание дробей

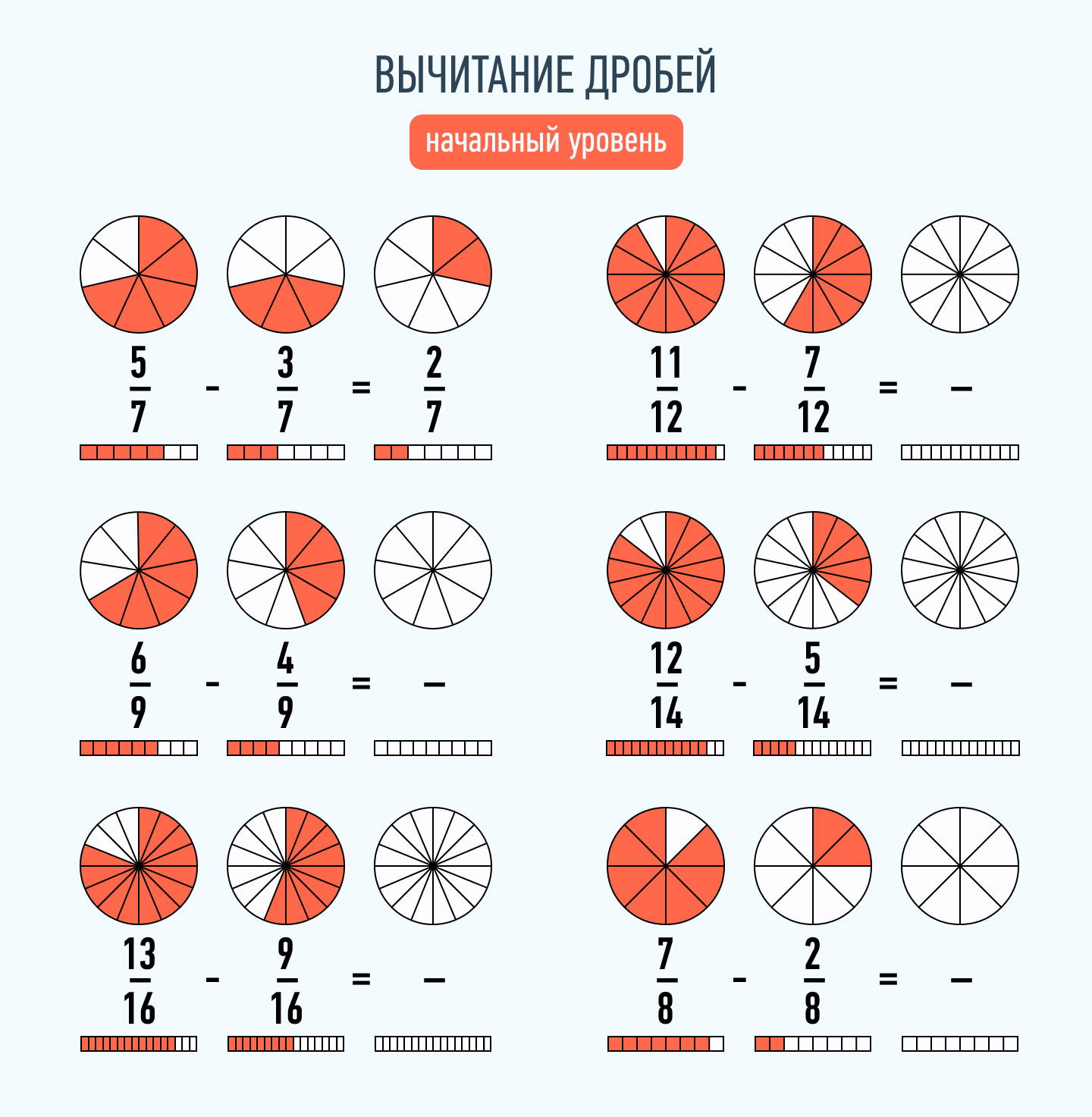
Эта операция проводится аналогично сложению. Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.

Пример:

7/9 — 2/9 = (7-2) / 9 = 5/9

Задание:

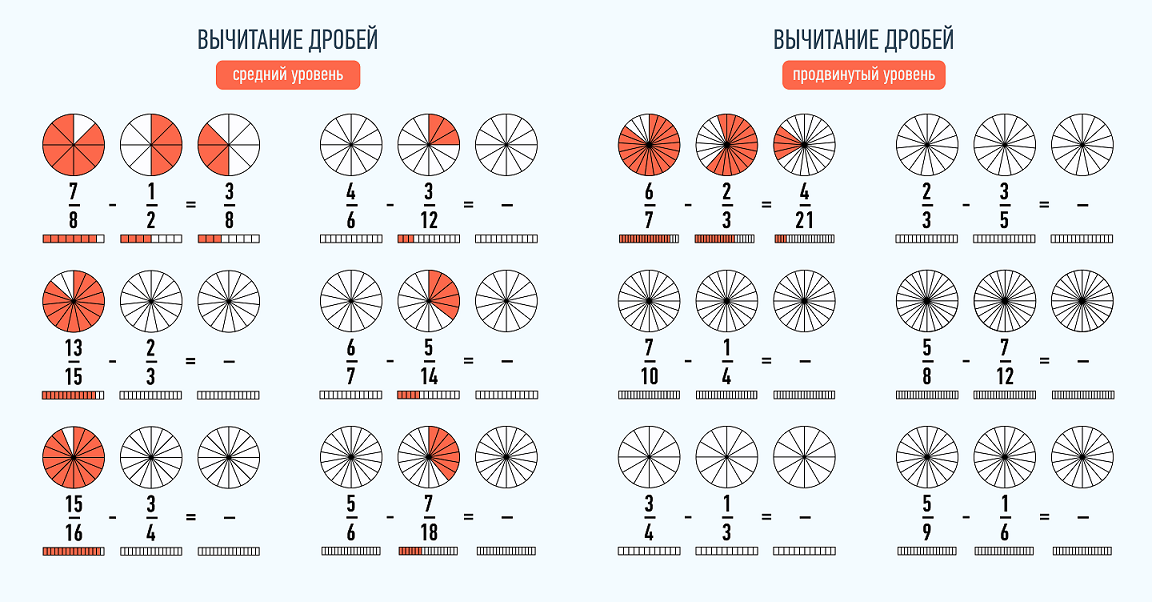
Выполни вычитание дробей с одинаковыми знаменателями:

Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.

Пример:

6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70

Задание:

Выполни вычитание дробей с разными знаменателями:

Умножение дробей

Существует два варианта умножения дробей. Рассмотрим каждый из них в деталях.

Умножение обыкновенных дробей

В этом случае числители обеих дробей перемножаются — это будет новый числитель. Знаменатели обеих дробей также перемножаются — это будет новый знаменатель.

Пример:

2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10

Если это возможно, то следует сократить дроби перед перемножением. Это облегчит дальнейшие действия.

Пример:

24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21

Умножение смешанных дробей

Чтобы это сделать, необходимо превратить дроби в неправильные и далее действовать по алгоритму, приведенному в первом пункте.

Пример:

4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24

Задание:

Выполните умножение дробей:

• 5/7 * 6/8;
• 6/11 * 2/3;
• 2 3/7 * 4 5/9;
• 4 6/7 * 7 9/10.

Деление дробей

Освоив умножение, с делением также можно справиться легко. Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый  знаменатель).

Пример:

4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7

Бывают ситуации, когда дробь нужно разделить на целое число. В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.

Пример:

5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18

Задание:

Выполните деление дробей:

• 6/11 : 3;
• 7/15 : 2;
• 9/12 : 4.

Сравнение дробей

Если сравниваются дроби с одинаковыми знаменателями, то очевидно, что большей будет та, числитель у которой больше.

Пример:

1/5 < 4/5, так как знаменатели одинаковы, а в числителе 1 меньше 5.

Если сравниваются дроби с одинаковыми числителями, то большей будет та, знаменатель у которой меньше.

Пример:

1/2 > 1/8, так как числители одинаковы, а в знаменателе 8 больше 2.

Дроби же с разными знаменателями так просто не сравнишь. Нужно сперва определить их общий знаменатель и привести к нему обе дроби. Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.

Пример:

Сравниваем дроби 2/5 и 1/10. Для этого приводим их к общему знаменателю — 10. Получаем 4/10 и 1/10. Теперь сравниваем дроби, уже имеющие одинаковые знаменатели: 4/10 > 1/10.

Есть один секрет, который нужно запомнить. Если одна из сравниваемых дробей неправильная, то она всегда больше правильной. Если подумать и вспомнить свойства дробей, то все становится понятно.  Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.

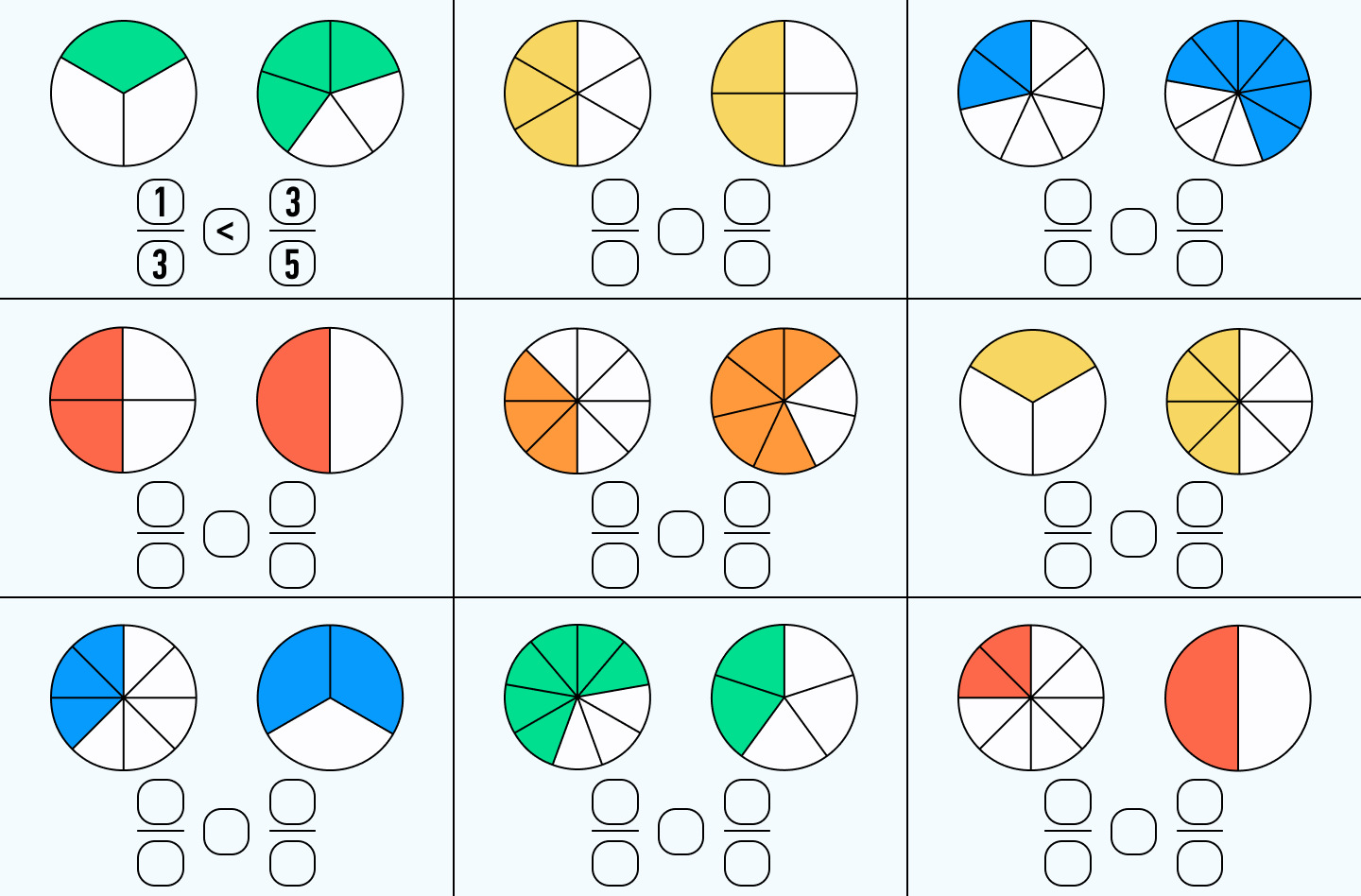
Задание:

Определите, какие дроби изображены на рисунке, и сравните их:

Итак, мы рассмотрели дроби, правила всех действий с ними. Надеемся, что наши объяснения и рекомендации будут очень полезны. Начинайте знакомить детей с дробями еще до школы. Хорошо усвоив эти понятия, ребенок без труда справится затем и с записью дробей, и с действиями с ними.